بازگشت نتیجه دار در پایتون
تاکنون, تنها زیر مجموعه کوچکی از پایتون را آموخته اید اما شاید جالب باشد که بدانید این زیر مجموعه کوچک یک زبان برنامه نویسی کامل است.
یعنی به وسیله این زبان می توانید هر چیزی را که قابل محاسبه است , بیان کنید.
هر برنامه ای که تاکنون نوشته شده می تواند تنها با استفاده از ویژگی هایی از زبان که تا این زمان آموخته اید باز نویسی شود.
(در واقع شما به تعداد محدودی از دستورات نیاز دارید تا بتتوانید واحد هایی همچون صفحه کلید, ماوس, دیسک ها و …را کنترل کنید.
اثبات این ادعا که اولین بار توسط “آلن تورینگ”انجام شده, تمرین قابل توجهی است او یکی از اولین دانشمندان علم کاامپیوتر است.
علارقم اینکه بعضی عقیده دارند “آلن تورینگ”یک ریاضیدان است, اما بسیاری از دانشمندان اولیه علم کامپیوتر با ریاضی شروع کردند.
بنابراین از آن به عنوان علم تورینگ یاد می شود.
اگر در جریان فرضیه محاسبات هستید, شانس دیدن اثبات آن را خواهید داشت.
برای اینکه به شما ایده ای بدهیم که با ابزاری که تاکنون آموخته اید چه کارهایی می توانید انجام دهید, تعدادی از تابع ریاضی تعریف شده به حالت بازگشتی را ارزیابی خواهیم کرد.
تعریف بازگشتی, شبیه به تعریف حلقوی است.
به این مفهوم که تعریف, شامل ارجاعی است به چیزهایی که تعریف شده اند.
یک تعریف حلقوی چندان مفید نیست:
Frabjuous
صفتی است برای شرح هر چیزی که frabjous باشد.
اگر تعریف فوق را در لغت نامه جستوجو کنید ممکن است آزرده شوید.
از طرف دیگر اگر به تعریف فاکتوریل ریاضی نگاه کنید, چیزی شبیه به عبارت زیر را خواهید دید:
این تعریف می گوید فاکتوریل ۰, ۱ است و فاکتوریل n برابر است با ضرب n در فاکتوریل n-1 بنابراین ۳ برابر است با ۳ تا ۲ که خود برابر ۲ تا ۱ و آن هم برابر ۱ در ۰ است.لذا نتیجه برابر با ۶ می باشد.
اگر بتوانید تابع بازگشتی چیزی را بنویسید , معمولا یک برنامه پایتون هم برای ارزیابی آن بنویسید.
اولین گام مشخص کردن پارامتر های تابع است.
با تلاش جزئی متوجه خواهید شدکه factorial یک پارامتر میگیرد:
اگر مقدار آرگومان تابع ۰ باشد, کافی است ۱ را باز گردانیم :
در غیر این صورت (این قسمت جالب برنامه است ) ما باید یک فراخوانی بازگشتی برای پیدا کردن فاکتوریل n-1 بسازیم سپس آن را در n ضرب کنیم :
روند اجرای این برنامه شبیه روند تابع countdown است .اگر ما تابع فاکتوریل را در بخش ۳ صدا بزنیم :
از آنجا که ۳ مخالف ۰ است , شاخه دوم را دنبال می کنیم که محاسبه مقدار فاکتوریل n-1 است.
از آنجا که ۲ مخلف ۰ است, شاخه دوم را دنبال می کنیم که محاسبه مقدرار فاکتوریل n-1 است.
از آنجایی که ۱ مخالف ۰ است , شاخه دوم را دنبال می کنیم که برگرداندن مقدار ۱ بدون هیچ فراخوانی بازگشتی دیگر است.
مقدار برگشتی (۱)در n , که برابر با ۱ می باشد , ضرب شده و نتیجه بازگردانده می شود.
مقدار برگشتی (۱)در n , که برابر با ۲ می باشد , ضرب شده و نتیجه باز گردانده می شود.
مقدار برگشتی (۲)در n , که برابر با ۳ می باشد , ضرب شده و ۶ را نتیجه می دهد. مقدار بازگشتی به اولین تابعی که فراخوانی شده باز می گردد.
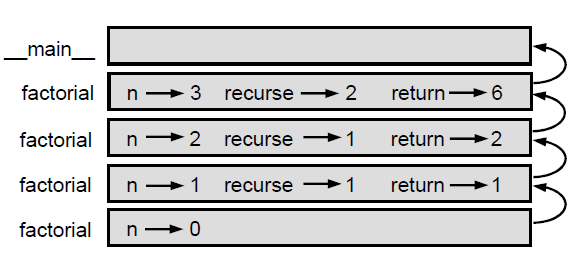
در شکل پایین آنچه را که نمودار پشته برای دنباله ای از فراخوانی های تابع نشان می دهد , ملاحظه می کنیم:
تحویل مقادیر بازگشتی به پشته بالایی در نمودار توسط پیکان هایی نمایش داده شده اند. در هر قاب مقدار بازگشتی result است که به وسیله n , recurse تولید شده است .
توجه کنید که در قاب آخر متغیر های محلی recurse و result وجود ندارند , زیرا شاخه سازنده آنها اجرا نمی شود.


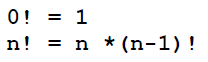


 مشاوره از طریق تلگرام
مشاوره از طریق تلگرام