مطالب آموزشی
دستور while در پایتون
دستور while در پایتون
while در پایتون
تا به حال دو برنامه NLINES و COUNTDOWN را که از بازگشت برای انجام عمل تکرار استفاده میکنند، دیدهایم. این گونه برنامه ها نیز تکرا نامیدده میشوند. از آنجا که عمل تکرار بسیار رایج است، پایتون چندین خصیصه زبان برای ساده تر کردن آن فراهم میکند.
اولین خصیصه ای که قصد داریم برسی کنیم، دستور WHILE است.
در اینجا چیزی شبیه به برنامه countdown رابا یک دستور while می بینید:
از آنجا که ما فراخوانی بازگشتی را حذف کرده ایم، این تابع بازگشتی نیست.
شما میتوانید دستور while را همان طور که در زبان انگلیسی بیان میشود، استفاده کنید.
این کد یعنی « تا وقتی که ۰ < n است، مقدار n را چاپ کرده و آنگاه ۱ را از آن کم کن. وقتی n به ۰ رسید، کلمه blastoffC! را نمایش بده.»
در اینجا روند اجرای یک دستور WHILE را به صورتی دیگر در پایتون
. ارزیابی شرط و به دست آوردن ۰ یا ۱
.اگر شرط FALSE (0( بود، از دستور WHILE خارج شو و دستور بعدی را اجرا کن.
. اگر شرط TRUE (1) بود،تمام دستورات موجود در بدنه را اجرا کن و به مرحله ۱ برگرد.
منظور از بدنه تمام دستوراتی است که در زیر عنوان قرار گرفته اند و دارای تو رفتگی یکسان هستند.
این روند را یک حلقه مینامند، زیرا مرحله سوم به صورت یک حلقه به مرحله اول پیوند داده شده است.
توجه کنید که اگر شرط در اولین برسی حلقه FALSE باشد، دستورات درون حلقه هرگز اجرا نمیشوند.
بدنه حلقه باید یک یا چند مقدار را تغییر دهد، به طوری که نهایتا شرط FALSE شود و حلقه پایان یابد.
در غیر این صورت حلقه برای همیشه تکرار میشود، که به این حالت حلقه بی انتها گفته میشود.
در مورد COUNTDOWN میتوانیم ثابت کنیم که حلقه پایان مییابد.
زیرا می دانیم که مقدار N متناهی است و می بینیم که در طول حلقه هر بار کوچکتر می شود بنابراین سرانجام به مقدار ۰ می رسیم.
در برخی موارد به راحتی نمی توان متناهی بودن حلقه را اثبات کرد:
شرط این حلقه ۱=! N است، بنابراین حلقه تا آنجا که N برابر با ۱ شود، ادامه می یابد چرا که این حالت شرط حلقه را FALSE می کند.
در هر بار اجرای حلقه، برنامه مقدار N را به عنوان خرجی چاپ می کند سپس زوج یا فرد بودن آن را برسی می کند.
اگر زوج باشد، مقدار N بر ۲ تقسیم می شود و اگر فرد باشد مقدار با عبارت ۱+۳ N جایگزین می گردد.
برای مثال اگر مقدار آغازین (آرگومانی که به تابع SEGUENCE فرستاده می شود) ۳ باشد، دنباله حاصل به این صورت خواهد بود:
از آنجا که N گاهی کاهش و گاهی افزایش پیدا می یابد، هیچ دلیل آشکاری برای رسیدن N به مقدار ۱ یا پایان برنامه، وجود ندارد.
برای برخی مقادیر ویژه N، میتوانیم پایان یافتن برنامه را تضمین کنیم.
برای مثال اگر مقدار آغازین توانی از ۲ باشد، آنگاه مقدار N تا وقتی که به ۱ برسد، در هر بار اجرای حلقه زوج خواهد بود.
در مثال قبل هنگامی که در دنباله به عدد ۱۶ رسیدیم، می توانیم مطمئن باشیم که این دنباله پایان می پزیرد(یعنی شرط حلقه ۱==N می شود)
صرف نظر از مقادیر ویژه، سوال جالب آن است که آیا می توانیم ثابت کنیم که این برنامه برای تمام مقادیر N پایان می یابد؟
تاکنون کسی نتوانسته این موضوع را ثابت یا رد کند.
نویسنده : زهرا رستمی




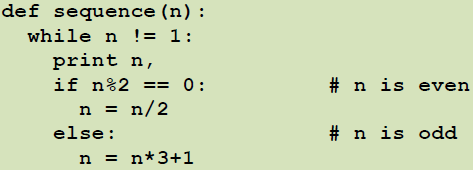
 مشاوره از طریق تلگرام
مشاوره از طریق تلگرام